Why Does the Derivative Equal Zero at a Maximum or Minimum?
Quadratic functions are one of the most important topics in algebra. They show up in classrooms everywhere and in real life more often than you might think. If you have ever noticed the arc of a basketball shot, the curve of a rollercoaster, or the shape of a satellite dish, you have seen a quadratic in action.
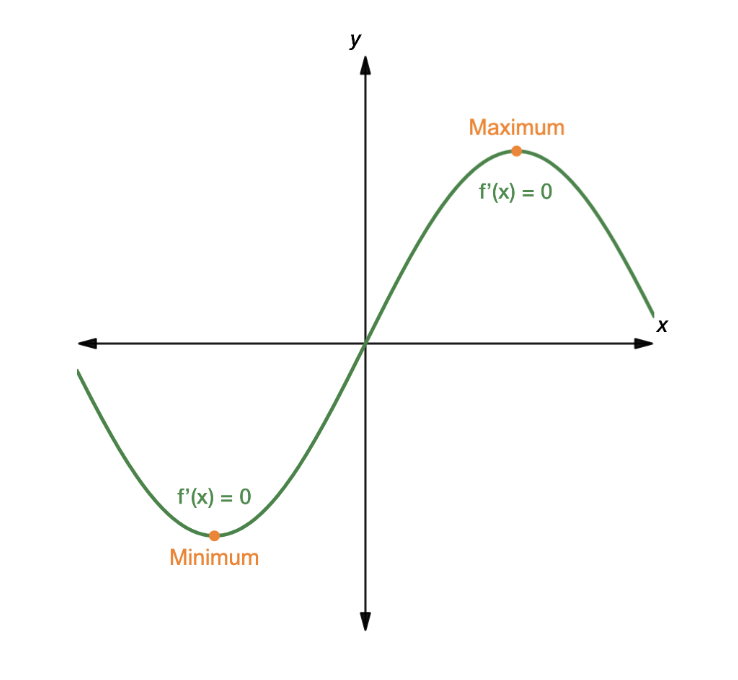
If you are in calculus, you have probably heard this rule: 
“At a maximum or minimum, the derivative is zero.”
It’s a powerful idea, but it can feel like a random fact until you understand why it is true. Let’s break it down step by step in a way that actually makes sense.
The big idea in one sentence
When a function reaches a smooth peak or valley, the graph levels out for a moment. That means the tangent line is flat. A flat tangent line has slope 0, and the derivative is the slope of the tangent line.
That’s it. Now let’s make it real.
Step 1: Remember what a derivative means
The derivative at a point tells you the instantaneous rate of change. Visually, it represents the slope of the tangent line at that point.
-
Positive derivative: the function is increasing
-
Negative derivative: the function is decreasing
-
Zero derivative: the tangent line is horizontal
Step 2: What “maximum” and “minimum” really mean
A local maximum is a point where the function value is higher than at nearby points.
A local minimum is a point where the function value is lower than that of nearby points.
Picture walking on a hill:
-
As you walk up, you are going upward. Your slope is positive.
-
At the top, you stop going up and are about to go down.
-
Right at the top, you are not moving up or down for that instant.
That moment of “not moving up or down” is the key.
Step 3: Why the slope must become zero at a smooth peak or valley
At a smooth local maximum:
-
Just before the maximum, the function is increasing, so the slope is positive
-
Just after the maximum, the function is decreasing, so the slope is negative
For the slope to switch smoothly from positive to negative, it must pass through 0.
The same idea applies to a smooth local minimum:
-
Just before the minimum, the slope is negative
-
Just after the minimum, the slope is positive
To switch smoothly, the slope must hit 0.
This is why the tangent line is flat at a smooth maximum or minimum.
Step 4: The formal statement (Fermat’s Theorem)
Here’s the math rule behind the idea:
"If a function has a local maximum or minimum at a point and is differentiable at that point, then the derivative there is zero."
The word differentiable matters a lot. More on that in a moment.
A quick example you can feel
Take a simple parabola.
f(x) = x^2
This function has a minimum at x = 0.
Now compute the derivative.
f′(x) = 2x
Plug in x = 0.
f′(0) = 2(0) = 0
At the minimum, the slope is flat. That matches both the graph and the logic.
Important: derivative = 0 does NOT always mean max or min
This is where many students get tripped up.
A point where the derivative is zero is called a critical point. Critical points are candidates for maxima or minima, but they are not guaranteed to be either.
Example:
f(x) = x^3
Derivative:
f′(x) = 3x^2
At x = 0:
f′(0) = 0
But the graph of x³ does not turn around at x = 0. It keeps increasing. That point is an inflection point, not a maximum or minimum.
So think of it this way:
-
Max or min (if smooth) ⇒ derivative = 0
-
Derivative = 0 ⇒ maybe a max or min, maybe not
You still need a test to confirm.
Turning point vs inflection point
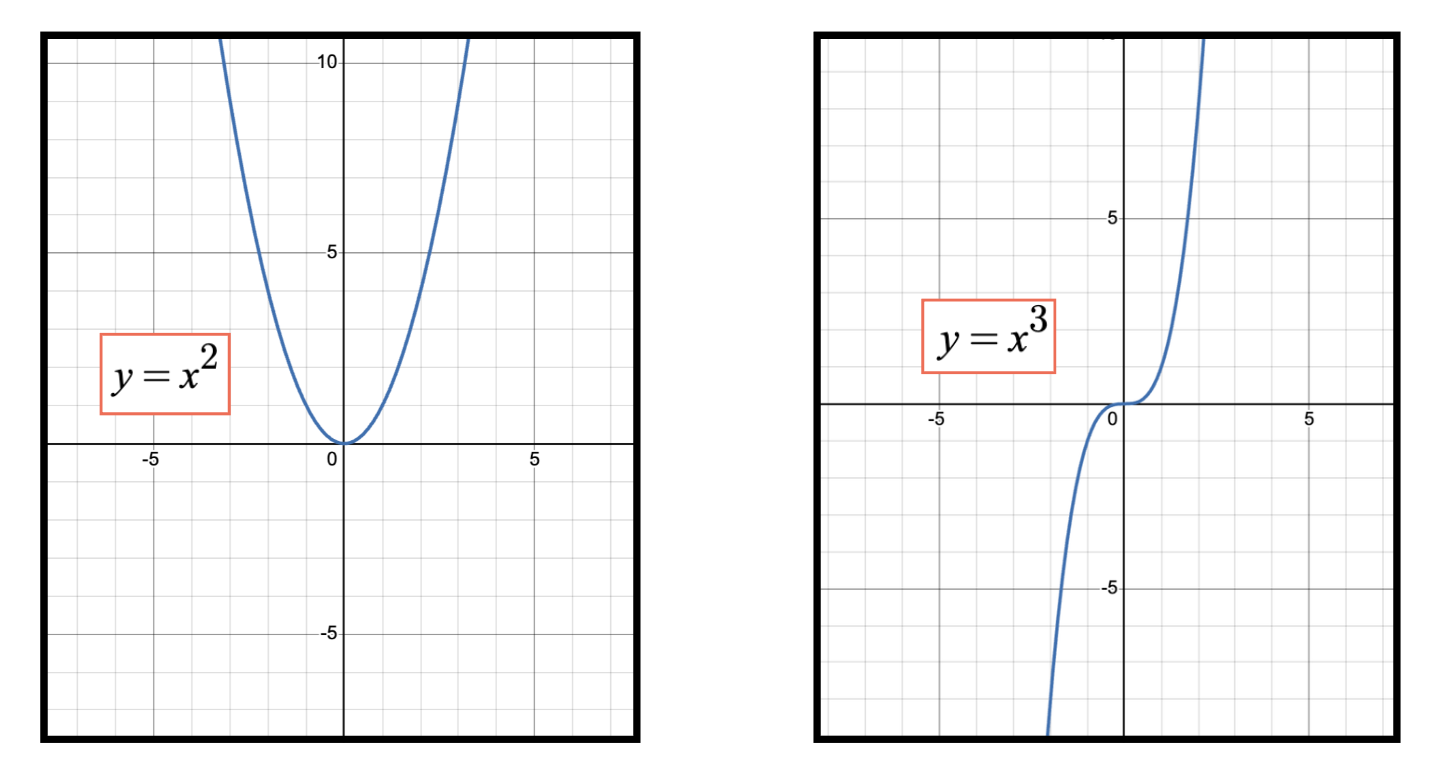
Not every point where the derivative is zero is a maximum or minimum.
The graph of x³ flattens at x = 0 but does not change direction.
Even more important: sometimes maxima and minima happen when the derivative is NOT zero
This happens when the graph is not smooth or when the point is an endpoint.
Case 1: Corners or cusps (not differentiable)
f(x) = |x|
This function has a minimum at x = 0, but the graph has a sharp corner. There is no single tangent line at that point, so the derivative does not exist there.
Case 2: Endpoints of an interval
When finding an absolute maximum or minimum on a closed interval like [a, b], the highest or lowest value may occur at the endpoints, even if the derivative is not zero there.
That’s why the full strategy in calculus is:
-
Check where f′(x) = 0
-
Check where f′(x) does not exist
-
Check endpoints
Quick checklist: how to find maxima and minima correctly
-
Find where f′(x) = 0
-
Find where f′(x) does not exist (corners, cusps, vertical tangents)
-
If the problem has an interval, check endpoints
-
Use a test to confirm:
-
First derivative test (sign changes)
-
Second derivative test (concavity)
-
Challenge Yourself
Try this one.
f(x) = x^4 − 4x^2
Step 1: Find the derivative
f′(x) = 4x^3 − 8x
Step 2: Set the derivative equal to zero
4x^3 − 8x = 0
Factor:
4x(x^2 − 2) = 0
Solve:
x = 0
x = ±√2
Step 3: Decide which are maxima and which are minima
Use the first derivative test to determine where the function is increasing and decreasing.
Multiple extrema
Graph of y = x⁴ − 4x²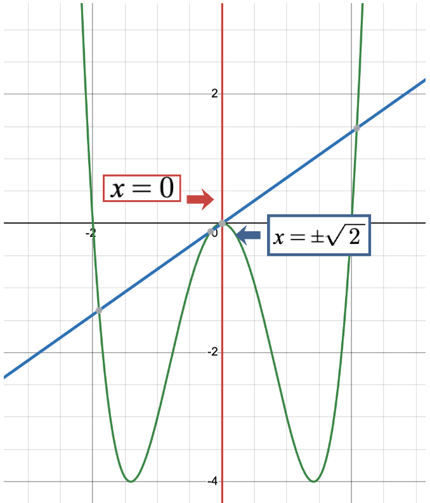
This graph shows how different critical points can represent maxima or minima depending on how the function changes direction.
How StarSpark helps you feel more confident with calculus
If you’ve ever looked at a calculus problem and thought, “I understand this in class, but it falls apart when I’m on my own,” you’re not alone. That gap between knowing the rule and trusting yourself to use it shows up most during quizzes, tests, and exam prep.
StarSpark is built to help close that gap. It walks you through problems like this step by step, connecting derivatives to graphs so you can see what’s actually happening, not just memorize what to do. As you practice, you start to recognize patterns, check your own reasoning, and feel more confident explaining why an answer works.
That matters when you’re reviewing for an exam, working under time pressure, or trying to decide which strategy to use. Instead of second-guessing yourself, you build the kind of understanding that helps you stay calm and focused when it counts.
If you want to try this style of guided practice for yourself, StarSpark offers a 30-day free trial, so you can explore concepts, practice problems, and exam prep at your own pace.




